11 ODEs: Applications

13 Mar 2018

After implementing a number of integrators for ODEs we are now in the position to solve some practical problems:

• projectile movement with air resistance
• realistic movement of a spinning baseball

For the problem that you should solve during the class, get the notebook¹ 11-ODE-applications-students.ipynb and see notebook 11-ODE-applications.ipynb for the full solution.²

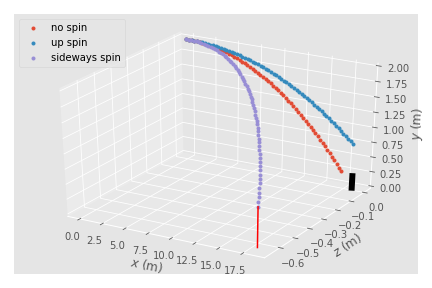
The baseball problem was live-coded from scratch during class and the notebook baseball_solution.ipynb is a cleaned-up and commented solution. The lesson showed how

1. to define the physical problem (obtain trajectory of a baseball with spin and air resistance)
2. to derive the underlying equations (Newton's equations of motions and the forces acting on the ball)
3. to adapt an algorithm to solve the equations (use RK4 for integrating the ODEs and express the problem in ODE standard form so that one can use ode.rk4())

4. to visualize and discuss the results (plot trajectories and assess the influence of spin)

   

Resources

• Computational Modelling: Chapter 3
• See Homework Assignment 7 (pdf) for a summary of Baseball Physics, extensions to the physical model (including the velocity-dependence of the quadratic drag coefficient and the "drag crisis" around typical baseball velocities), and links to the literature.

---

Footnotes